
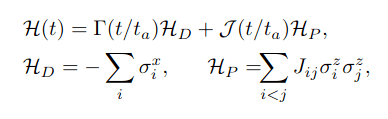
Problem:
Time evolution of the transverse field Ising model
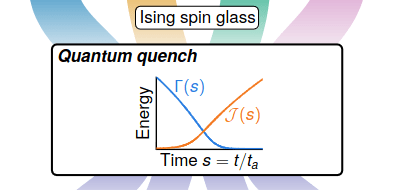
QPT between the two phases, topology dependent universal behaviour
Random
Real materials
Generative AI
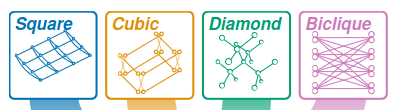
Geometries:
Dimension
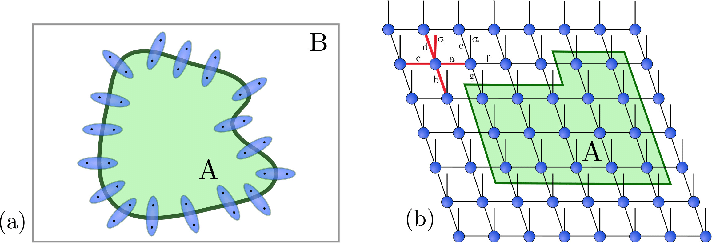
Area law entanglement
Expensive classical simulations
Methods:
Classical
Quantum


- Quantum annealing processors:
- Advantage 1 (ADV1)
- Advantage 2 (ADV2)
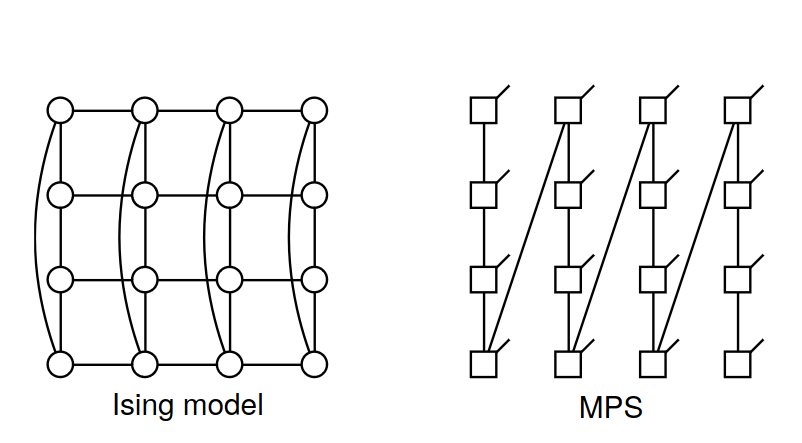
- Tensor Networks methods:
- MPS
- PEPS (Proj.-Ent.-Pair States)
- Machine learning:
- NQS (Neural Quant. State)
Review of the methods
Classical
MPS
Benchmark for small system sizes
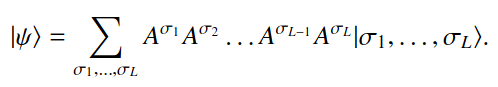
Each
is a matrix of dim.
where
is the bond dimension.
MPS in a so-called "canonical" form (or isometry):
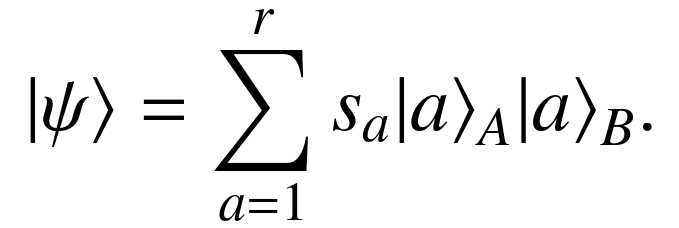
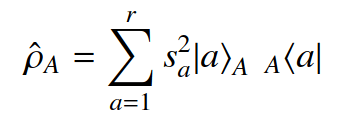
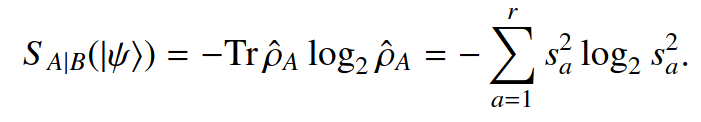
Discard states optimally in the sense of the vN EE
Canonical form always in 1D, not for higher dimensions
Lose the area law in 2D!
Review of the methods
Classical
MPS
Benchmark for small system sizes
Time dependent variational principle (TDVP)
: Product state obtained by DMRG
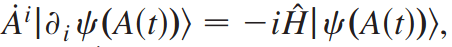

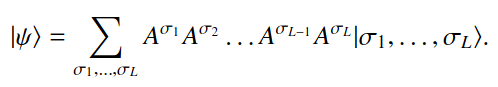
Each
is a matrix of dim.
where
is the bond dimension.
Review of the methods
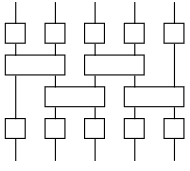
Classical
PEPS

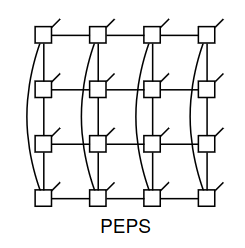
TN matches system's geometry
Area law of entanglement in 2D
TN contraction is expensive
No canonical form
Trotterized time evolution (quantum circuit):
Review of the methods
Classical
PEPS


TN matches system's geometry
Area law of entanglement in 2D
TN contraction is expensive
No canonical form
Trotterized time evolution (quantum circuit):
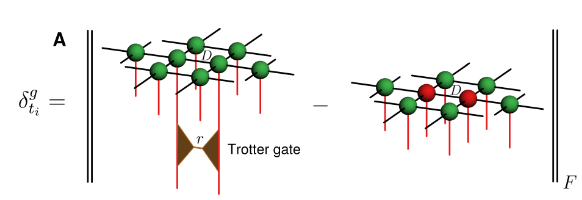
Minimization step to keep the bond dimension constant
Review of the methods
Classical
NQS
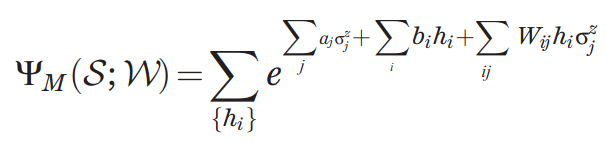
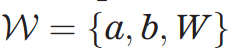
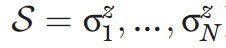
- Parameters:
- Hidden spin variables
- Physical spin variables:
Restricted Boltzmann Machine
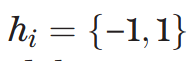
- Fails after short times (long range correlations)
- Lack of convergence for
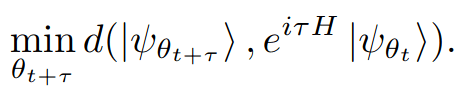
Review of the methods
Quantum
Quantum Annealing
1. What is a Quantum Annealer?
Answer to an optimization problem
Universal Quantum Computing
Sampling problems over the energy landscape
Review of the methods
Quantum
Quantum Annealing
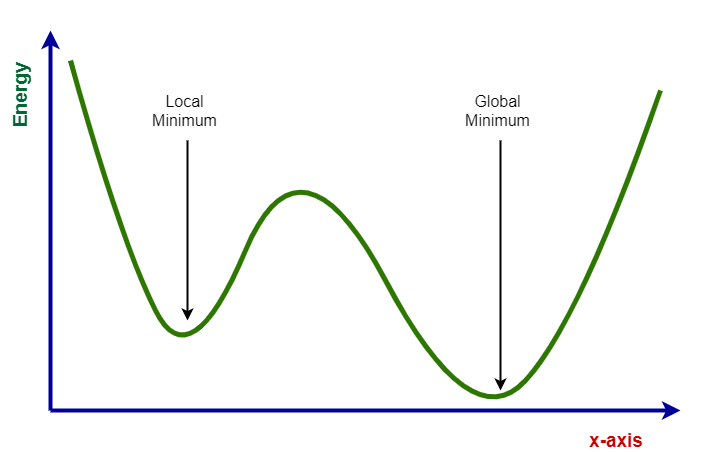
2. How does it work?
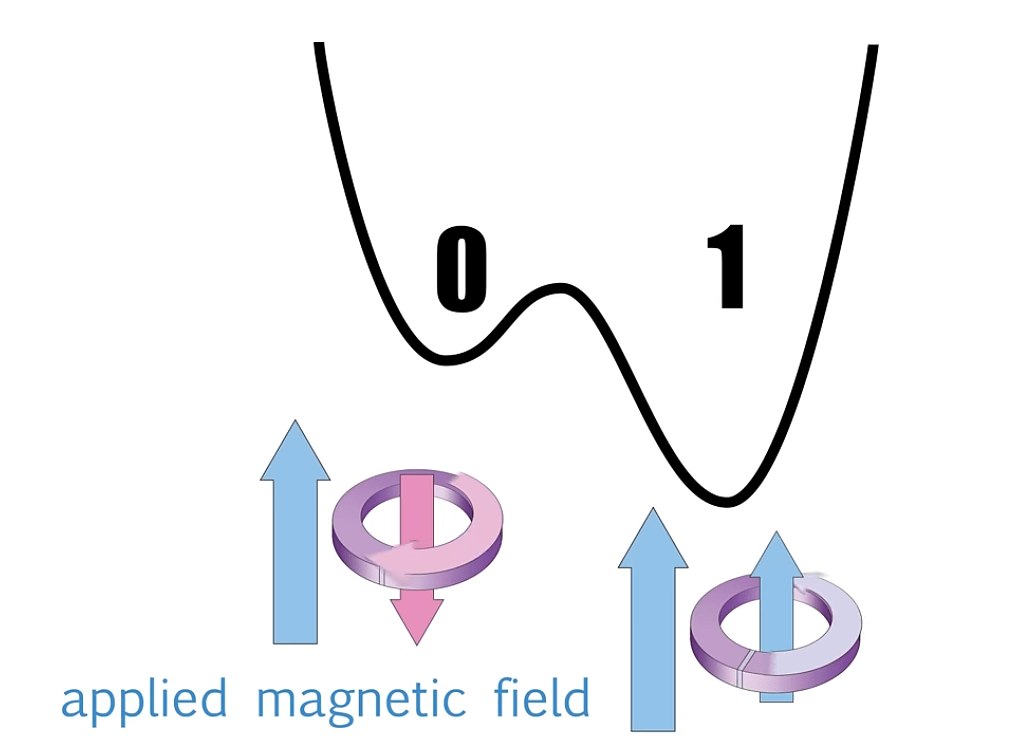
Change local minima
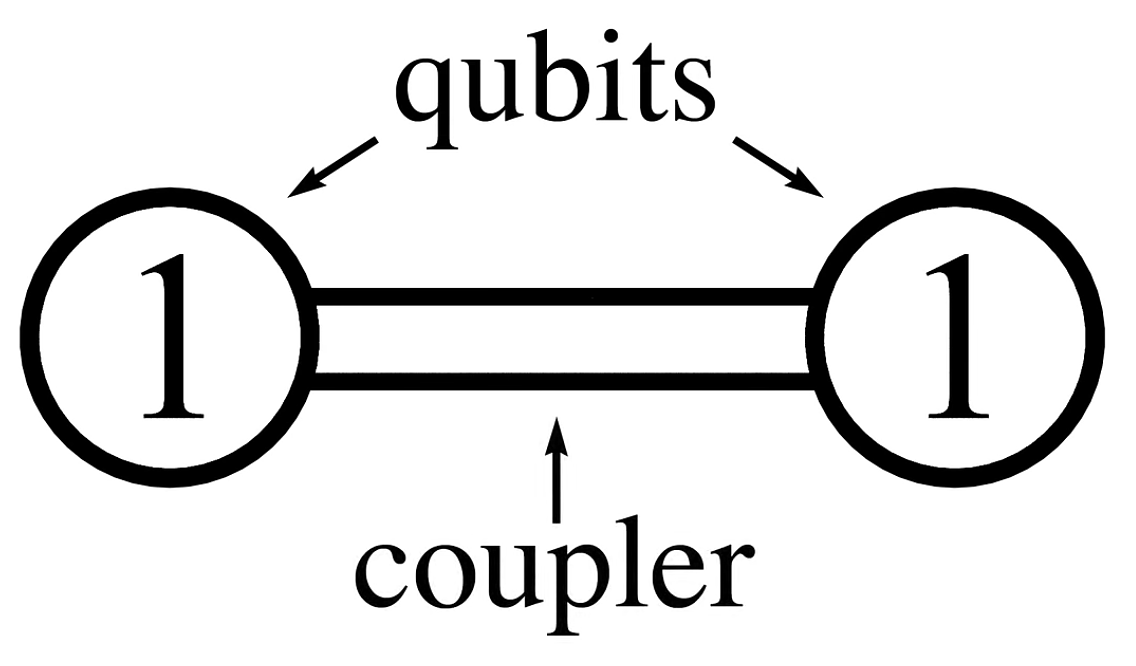
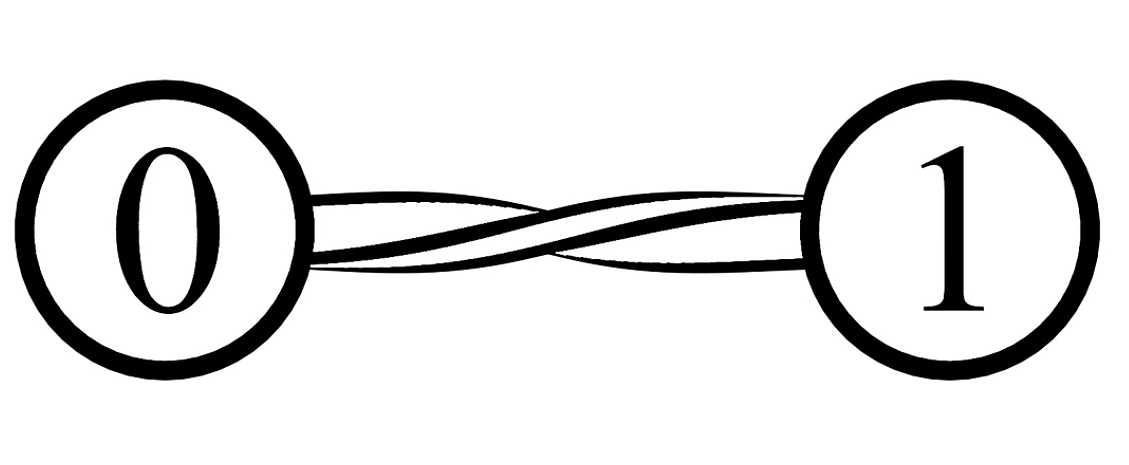
Couple states of different qubits
Directly acts on the energy landscape
Review of the methods
Quantum
Quantum Annealing
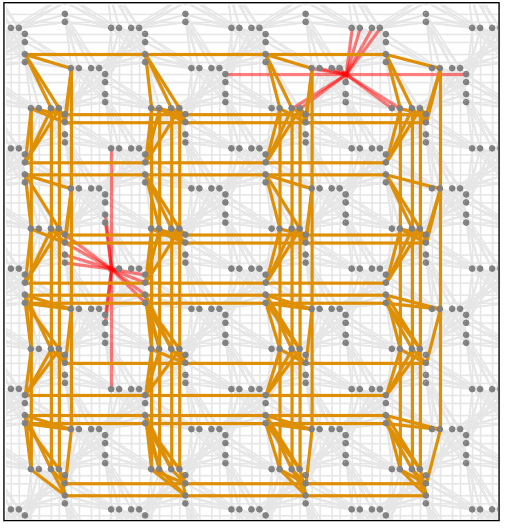

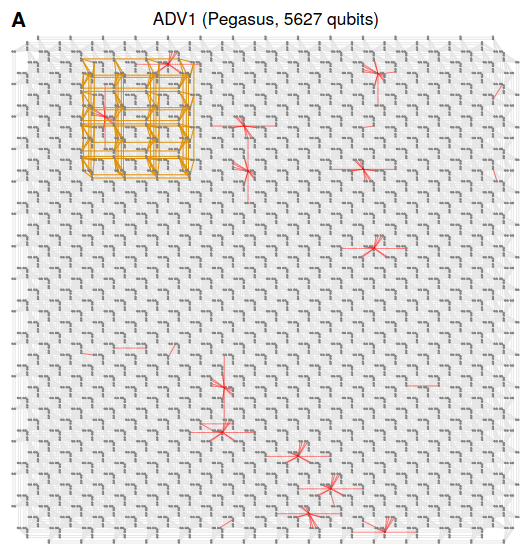
Radio-frequency
Superconducting
flux qubits (rf-SQUID)
Cubic dimer
Review of the methods
Quantum
Quantum Annealing
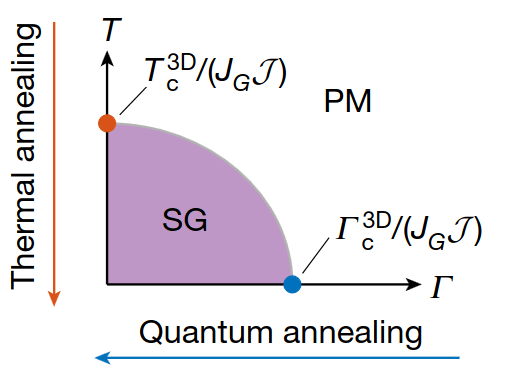
3. Annealing
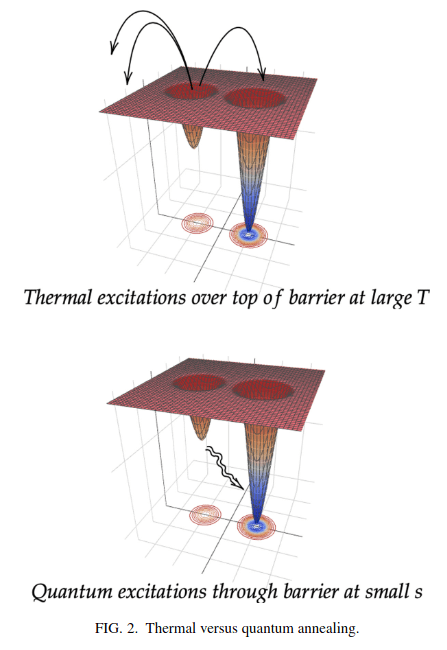
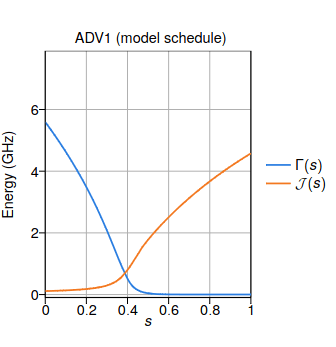
Change the energy landscape over time
Reach the final ground state
Initialize in a superposition of states with
Results
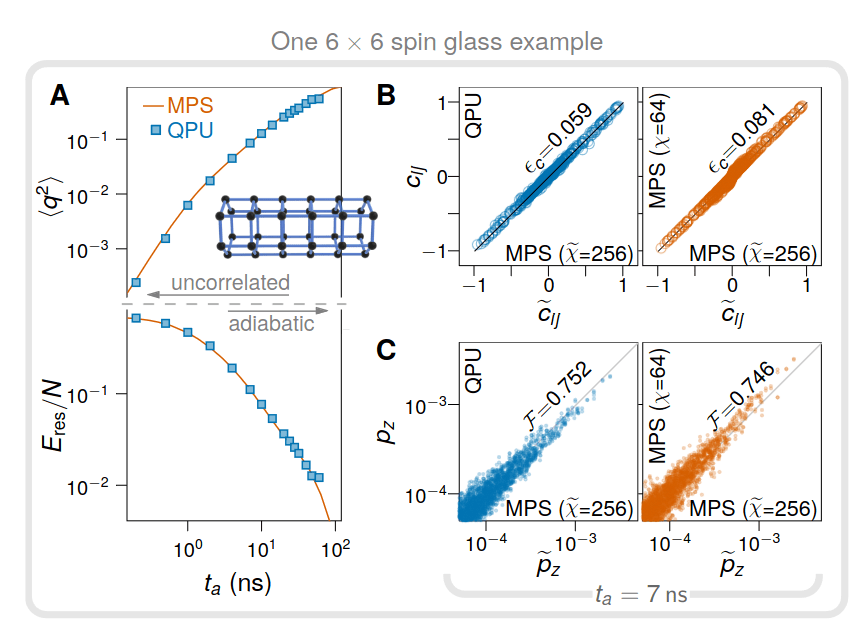
Benchmark the QPU
- Residual energy
- Spin-glass order parameter
- Classical fidelity (norm)
probability of state




Results
Benchmark the QPU
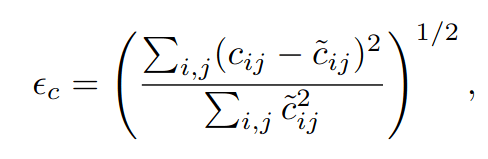
- Correlation error:
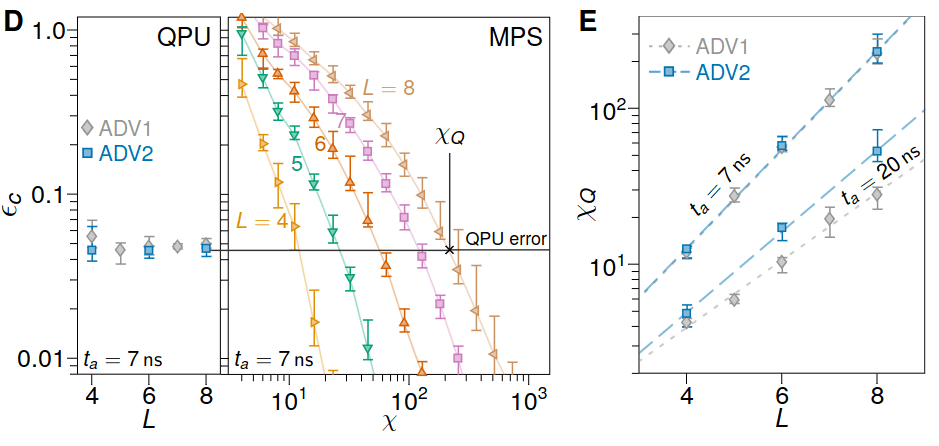
Equivalent QPU bond dimension
Results
Comparison to classical
- NQS didn't even work
- MPS serves as a ground truth
- PEPS up to 8 x 8
2D
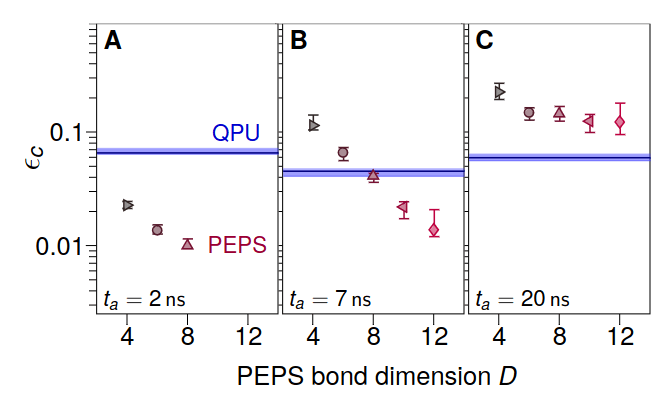
Limiting case for QPU
D>2
- MPS serves as a ground truth
- Nothing else worked
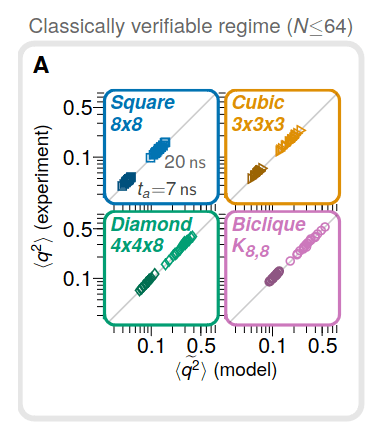
Results
Supremacy?
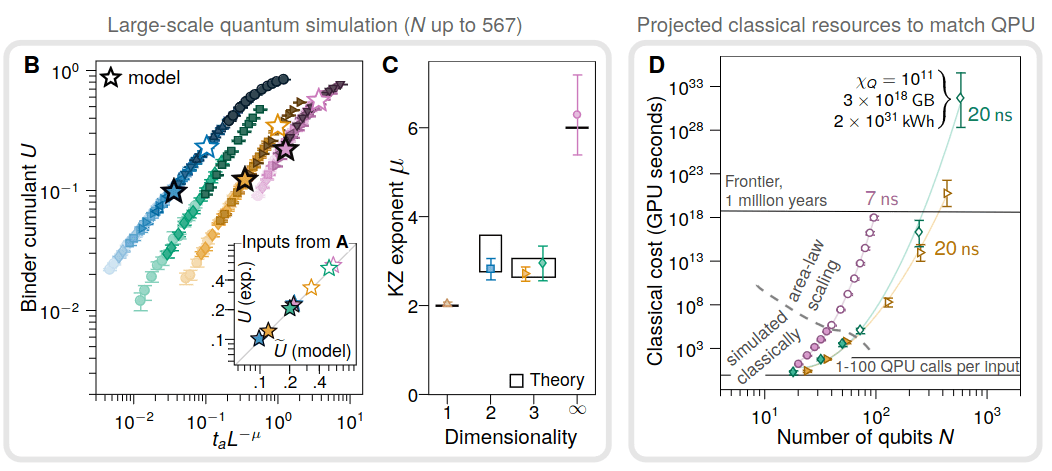
following an area law
scaling for the considered systems
Achtung!
MPS bond dimension doesn't have the area law scaling
Still room for improved classical simulation ...